Table of Contents
The complexity of an algorithm
Suppose you’d like to apply one of several algorithms to solve a problem. How to figure out which algorithm is better? You might implement these algorithms, start many times, and then analyze the time of solving the problem. However, this approach compares implementations rather than algorithms. There is no guarantee that the results will be the same on another computer.
We use the Big O notation to classify algorithms according to how their running time or space (e.g. in memory or on disk) requirements grow as the input size grows. It does not depend on implementation details such as programming language, the operating system, the hardware, or programmer skills, and other implementation details. We will focus on the time complexity first.
The Big O notation is written as O(T(n)) and consists of two parts:
- T(n) is a time complexity function that describes how the running time grows as the input size grows;
- the symbol O means that, when the input is large enough, the running time grows not faster than a function inside the parentheses.
The Big O notation has some essential features:
- it describes the upper bound of the growth rate of a function and could be thought of the worst-case scenario;
- it describes especially well the situation for large inputs of an algorithm, but it does not care about how well your algorithm performs with inputs of small size.
In practice, an algorithm may work even better than Big O shows, but definitely not worse.
Common growth rates
Here is a short list of some common notations sorted from the best O(1) to the worst O(2n) time:
- Constant time: O(1). The number of required operations is not dependent on the input size. Examples: accessing an element of an array by its index, calculating the sum of arithmetic progression using the formula, printing a single value.
- Logarithmic time: O(log n). The number of required operations is proportional to the logarithm of the input size. The basis of the logarithm can be any; that’s why it’s not written. Example: the binary search in a sorted array.
- Square-root time: O(sqrt(n)). The number of required operations is proportional to the square root of the input size.
- Linear time: O(n). The number of required operations is proportional to the input size, i.e. time grows linearly as input size increases. Often, such algorithms are iterated over a collection once. Examples: sequential search, finding max/min item in an array.
- Log-linear time O(n log n). The running time grows in proportion to n log n of the input. As a rule, the base of the logarithm does not matter; thus, we skip it.
- Quadratic time: O(n2). The number of required operations is proportional to the square of the input size. Examples: simple sorting algorithms such as bubble sort, selection sort, insertion sort.
- Exponential time: O(2n). The number of required operations depends exponentially on the input size growing fast.
The following picture demonstrates the common complexity functions (without O).
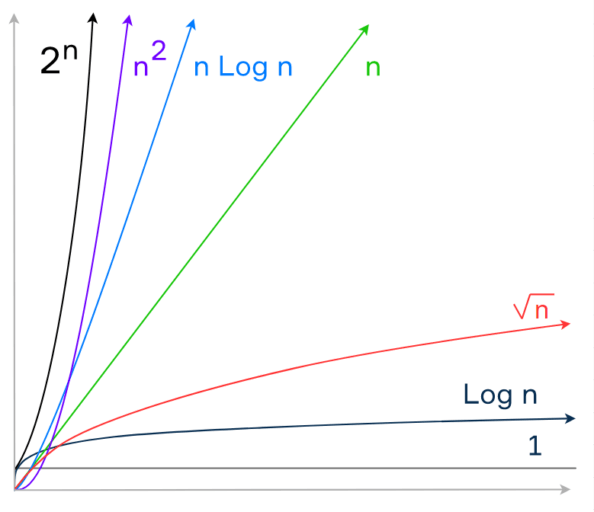
As you see, an algorithm with the time complexity O(n) is better than an algorithm with the time complexity O(n2) because the linear function grows slower than the quadratic one. However, an algorithm with the complexity O(log n) is better than both of them. The algorithm with the complexity O(2n) may need too much time to solve a problem even for a small input size. As a rule, we don’t use such algorithms in practice.
Space complexity
Interestingly, we can use the same big O notation for estimating the required memory for running algorithms. Suppose an algorithm has O(n) space complexity that means the required memory is proportional to the input size.
Conclusion
The big O notation is a crucial tool to evaluate the performance of algorithms and compare them. We can use it to evaluate both time and memory complexities. It is essential this notation classifies an algorithm rather than gives you a real running time in seconds or required memory in megabytes. You also should understand the difference between the standard complexity functions.